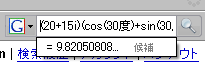えむもじらさまのこちらの記事で知ったのですが、 Firefox の Google 検索窓に数式を入力すると、サジェストとして Google 電卓による答えを表示してくれるんですね！これは凄い。あまりに凄いのでぜひネタにしようと思ったのですが、 Google 電卓そのものについてはgoogle電卓リファレンスさまをはじめとして、詳しく解説しているサイトがたくさんありました。そこで、一般的な使い方は先達の方々におまかせして、この記事ではプログラミングの際に便利な技をいくつかご紹介することにしました。仕事柄、後半はイレギュラーな座標計算に走っていますが、見過ごしてやってください。

Google 電卓では、 "計算式 in 単位" とすることで答えを指定した単位で表示できます。また、数値にも単位を付けることができます。容量計算などはお手の物です。

256 bits in bytes -> 32 bytes
10 Mb in bytes -> 1310720 bytes
1 MB + 256 bytes in bytes -> 1048832 bytes

"KB" はキロバイト、 "Kb" はキロビットになるのでご注意を。

単位変換の応用として、ボーレートに時間を掛ければその時間で転送できるデータ量になります。同様にして、データ量をボーレートで割れば転送に必要な時間、データ量を時間で割れば必要なボーレートが算出できます。

64Kbps * 10 minutes in MB -> 4.6875 メガバイト
16 MB / 64 Kbps in minutes -> 136.533333 minutes
16 MB / 10 minutes in Kbps -> 218.453333 Kbps

データ量と同様、 "bps" は bit per second, "Bps" は Byte Per Second です。

単位変換と同様に基数も変換できます。

90 in octal -> 0o132
0o132 in hex -> 0x5A
0x5a in binary -> 0b1011010
0b1011010 in decimal -> 90

超便利！（゜∀゜）

時間も変換できます。DNS レコードなどのタイムアウトを設定するときや、 JavaScript で Date オブジェクトの時間を操作したいときに便利でしょう。

10 days in seconds -> 864000 seconds
2 weeks + 3 days in seconds -> 1468800 seconds

months, years なども使えますが、これらは日数が確定しないため、小数点値になっています。

プログラムとはあまり関係ないかもしれませんが、「えふえふとぅえるぶ」ってどう書くんだっけ、なんてときに（笑）

64 in roman -> LXIV

65536 って英語でなんていうんだ、なんてときに。

65536 in English -> sixty-five thousand five hundred thirty-six

ただし言語が英語のときのみ使えるので、 URL に CGI パラメータとして "hl=en" を付加してください。こんな感じで。ちなみに日本語（hl=ja）では漢数字に変換する "? in 日本語" が使えます。こんな感じで。

n 個の集合から m 個を取り出したとき、順不同でいくつのパターンがあるかを計算できます。いわゆる組み合わせの数です。ちなみに私は数学嫌いですが、なかでも確立統計はいちばん嫌いです。

例えば、 10 人のキャラクターから 4 人を選んでパーティーを組むとき、その組み合わせは・・・

10 choose 4 -> 210

210 通りだそうです。

単位に度と radian が使えるので、面倒なラジアンと度の変換をまかせることができます。

90 度 in radian -> 1.57079633 radian
1.57079633 radian in 度 -> 90 度
sin(90 度) -> 1

言語が英語のときは、「度」の代わりに "degree" が使えます。

実数部を X 座標、虚数部を Y 座標と考えると、 2 次元ベクトルの演算が可能です。まず加算・減算は素直にできます。

(X1+Y1i)+(X2+Y2i)
(X1+Y1i)-(X2+Y2i)
例：(1+2i)+(3+4i) -> 4 + 6 i

さらに、以下の式の実数部が内積、虚数部が外積の値になります。

(X1-Y1i)*(X2+Y2i)

さりげなく唐突に変数を導入していますが、上記の X1, Y1 などは数値に置き換えてください。以下同様です。

acos が使えるので、内積からベクトルのなす角を算出できます。ただ、複素数から実数部のみを取り出すのが面倒なので、内積は普通に要素ごとに計算したほうがいいと思います。

acos((X1*X2+Y1*Y2)/(sqrt(X1^2+Y1^2)*sqrt(X2^2+Y2^2)))

答えはデフォルトでラジアン単位なので、必要に応じて単位変換してください。

さらに、複素数の掛け算の応用で回転計算もできます。座標 (X, Y) を原点中心にθだけ回転させるには、以下のようにします。

(X+Yi)*(cos(θ)+sin(θ)i)

θはデフォルトでラジアン単位なので、度数で指定するときは "90度" のように単位を付けてください。

複素数の割り算もサポートしているので、 2 点 (X, Y), (X', Y') が与えられたとき、 (X, Y) を (X', Y') に写像する直行変換を簡単に算出できます。ちなみに、直交変換とは回転と一様なスケーリングを伴う変換と考えてよいかと思います。

(X'+Y'i)/(X+Yi)
-> 答えを a + bi として、以下の行列が求める直交変換となります。
     | a -b |
     | b  a |

当然ながら、 (X, Y) != (0, 0) でなければなりません。

有名なネタですが、一応、載せておきます。

人生、宇宙、すべての答え

ディープソートがすべての答えを与えてくれます（笑）。

とりあえず、思いつくものを並べてみました。今日は眠いのでここまで。また思いついたら追記していきます。他にも面白い使い方がありましたら、ぜひコメント・トラバしてください！